The powerful maths learning strategies from Stanford University online course will help anyone achieve at the highest levels in maths.
In part 1, I summarised how our mindset, beliefs and experiences shape how we learn maths, check it out before you continue here.
So what separates people who are high maths achievers from those who are not?
Here’s a summary of key 5 learning strategies:
Interact with numbers flexibly
Talk about maths reasoning
See connections in maths
Make sense and use intuition
Always look for the big idea
Interact with numbers flexibly
The first maths learning strategy is number felxbility. What does this mean? The course demonstrates this by asking:
Work out 18 x 5 in your head without using paper or a calculator.
Have a go before reading the next bit…
The point of this exercise was not about getting the right answer. It was to show how people used different pathways to get to the answer.
Here are 5 different pathways:
Method 1
10 x 5 = 50
Then 8 x 5 = 40
Add together to get 90
Method 2
20 x 5 = 100
Then 2 x 5 = 10
Subtract 10 from 100 = 90
Method 3
Double 18 to get 36
Then double 36 to get 72
Add 18 to 72 = 90
Method 4
Halve 18 to get 9
Than 9 x 5 = 45
And 9 x 5 = 45
Add together to get 90
Method 5
9 x 10 = 90
Because 9 x 10 is the same as 18 x 5
You can watch, Jo Boaler, Professor of Mathematics Education at Stanford University, visually represent the different methods here.
I used the first method. Which pathway did you use?
It blew my mind to see the other pathways people used to work out the answer because I hadn’t thought of them. Back in my school days, I was taught there was only 1 way of solving a problem.
All problems can be solved in different ways. Number flexibility is being able to work with numbers and see what they are made of, and combine them in different ways. This is also known as number sense.

Here’s what I’ll be encouraging my daughter to do.
When you’re learning maths in school, if a teacher shows you a method, ask yourself what are the other ways of solving this problem.
And practice numbers flexibly by asking, “Is there more than one way of solving this?” Or “Let’s see how many different ways we can come up with to find 16 x 4.”
Talk about maths reasoning
When I was in school, maths was taught like this.
The teacher stands at the front, write the method to work out a problem on the board. Then tells the class to turn to page so and so in the text book, and do the exercises on your own, using the method on the board.
Does that sound familiar?
But it turns out working together, collaborating and talking about the problems you’re trying to solve is an important part of maths learning.
“When you talk about maths you have access to a different level of understanding than when you just read questions or work through them on your own.”
Jo Boaler, Professor of Mathematics Education at Stanford University
The importance of maths reasoning is shown in a study by Uri Treisman, Professor of Mathematics at The University of Texas.
He found that many students were failing Berkeley calculus classes and leaving. When he looked into those who were failing and those who were not, the only difference he found was this.

The successful students worked on maths as they ate dinner at night or they met in study groups to work on the problems together.
Those who were dropping out of classes were people who studied and worked on maths alone.
Reasoning is also important not just in the classrooms, but also in today’s tech world where jobs require the use of maths thinking.
Many companies now have big data and are looking for people to ask questions of the data, use maths to gain insight, connect with each other’s thinking to create new ideas, and make mathematical breakthroughs.
When you’re helping your child with their maths practice, encourage them to verbalise what they think the question is asking. What strategy they chose to use? Is there any other ways of solving the problem?
Talking about maths reasoning will help your child understand maths deeply, and also prepare them for maths in the world and in the jobs of the future.
See connections in maths
Studies have found that people who do well in maths are those who make connections and see maths as a connected subject. And the people who don’t do well are those who see maths as a lot of isolated methods.
To illustrate the connected web-like nature of maths, watch Jo Boaler give a tour of mathematical connections here.
The tour started off with fractions, made a table, drew graphs, then went into geometry and transformational geometry. It looked at dilation before touching on algebra and thinking about a slope. All these maths areas were connected to one big idea—expressing a proportion or a relationship.
So why is seeing maths as a connected subject important?
PISA (Programme for International Student Assessment) is an international study covering 80 countries, done every 3 years, to provide comparative data on 15-year-olds’ performance in reading, maths, and science.

Their study on maths achievements found differences in mindset, thinking and strategies used between high achievers and low achievers.
The lowest achieving students were those with a fixed mindset, thinking that you are either good at maths or not. They also thought of maths as a series of separate topics, and used memorisation strategy to learn methods.
The highest achieving students were those with a growth mindset, those who believe they can increase their abilities through effort, good strategies, and support from others. They approached maths by thinking about the big ideas, used positive strategies, made connections and didn’t rely on memorisation.
When helping your child with maths learning, here are some questions you can ask to encourage them to think about the connections in maths.
Why does that make sense?
How does this work?
How is this connected to other methods or areas of maths?
Make sense and use intuition
Using intuition in maths is definitely not something I was taught in school. How does this maths learning strategy help?
To make sense of maths—when approaching a maths problem, instead of jumping in to solve it with a formula, pause and ask yourself, “What do I know is true and what do I think is going on here?”
To illustrate why it’s important to make sense of maths using intuition, here’s a maths problem two of the Stanford students worked on together.
You need to fill your aquarium with salt water. You need to add 1/4 of a large bottle of salt water, but you only has 4 small bottles. If 4 bottles are 2/3 of a large bottle, how much of the small bottles should you use?
Rather than thinking about a formula or method, they drew out the problem to make sense of the question. And by doing so, it demonstrated the power of visuals in maths.
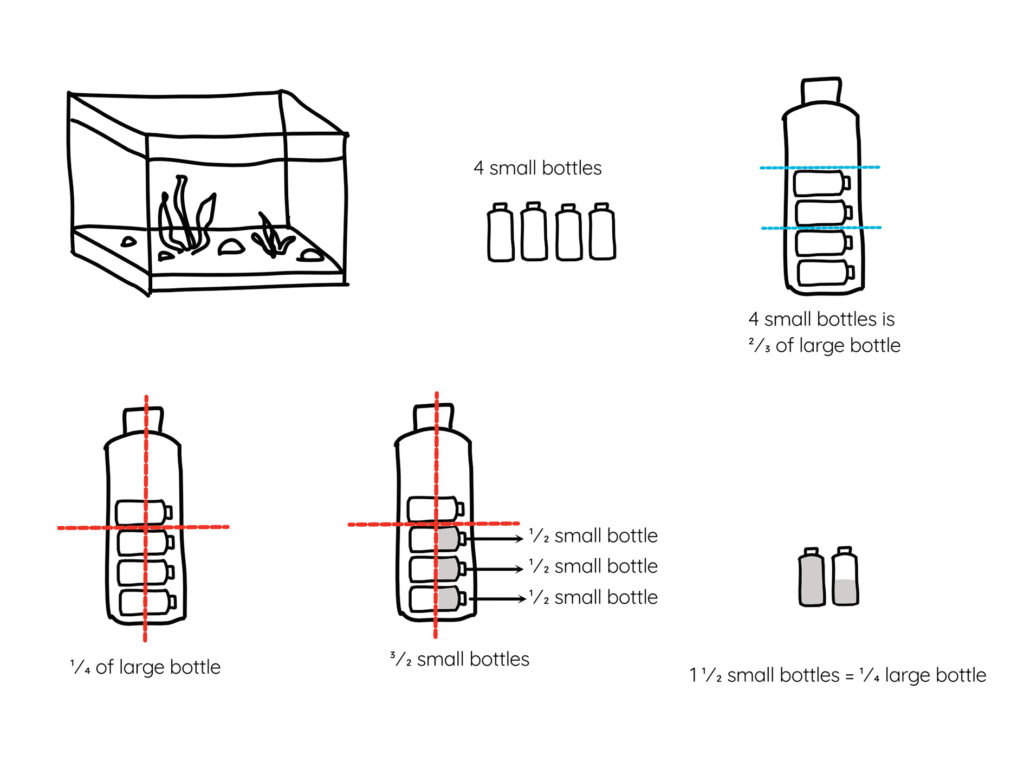
By drawing or visualising the problem—like talking—it gives access to understanding.
To make sense of maths and to use intuition, encourage your child to draw, use visuals or physical objects to represent the maths problem they’re working on.
Always look for the big idea
As shown in the study by PISA, the highest achieving students in maths were those who didn’t rely on memorising methods, they were students who thought about the big ideas.
In a typical maths class, you might be taught that to calculate the circumference of a circle, you use the formula—diameter times pi. So you might try to memorise pi which is a really long number: 3.14159265358979323846…
You practice on questions where you calculate the circumference of different circles by substituting in numbers using the formula, but completely miss the big idea.

Whatever the size of a circle or sphere, when you take the circumference, then you divide that by the diameter, you always get three and a little bit. And that relationship always gives you pi, no matter how big the circle is. In every circle, the diameter wraps around the circle 3.14 times.
Understanding math is about learning the big idea rather than getting lots of small questions right. Always ask yourself, what is the idea here? What is always true?






